Fractions another way of saying a part of something.
Simplifying or Reducing Fractions
Adding Fractions with the Same Denominator
Adding Fractions with Different Denominators
Subtracting Fractions with the Same Denominator
Subtracting Fractions with Different Denominators
What are fractions?
A fraction is another way of saying a part of something. If you had a pie and cut it so you had 4 equal amounts then you would have cut it into quarters. If you then ate one of those quarters you would have 3 quarters (3/4) left which is a fraction of the original cake. Three quarters is written as a fraction below.
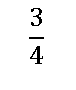
The top number is known as a numerator while the bottom number is called a denominator.
Calculating Fractions
What if you had £500 and you had to pay 1/5 in tax leaving 4/5 to be divided between you and your business partner. So how would you calculate how much you would get? First you would divide £500 into fifths which is 5 lots of £100. One fifth (or £100) would be given to the tax man while you and your business partner get 2 fifths each, so that’s 2 lots of £100. Therefore 2/5 of £500 is £200.
Now try 2/3 of £21. First we divide 21 by 3 giving us 7 and then we multiply the 7 by 2 giving us 14. So 2/3 of £21 is £14.
Equivalent Fractions
An equivalent fraction is when the comparability of the numerator (top number) and the denominator (the bottom number) of two fractions are the same.
Let’s take two seemingly different fractions.
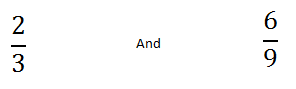
At first sight these two fractions may seem to have no connection but a second look may reveal that the numerator and denominator of the second fraction is the same as the first, just multiplied by three (2 x 3 = 6 and 3 x 3 = 9). So why is this important? Well the two fractions amount to the same thing as shown below.
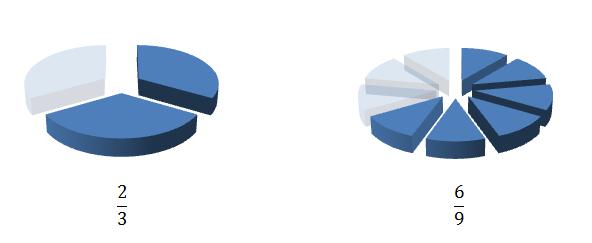
So although the two fractions appeared to be different they actually amount to the same thing. When this happens we say that they are equivalent fractions.
Simplifying or Reducing Fractions
Sometimes fractions can look rather large and complicated such as:-
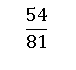
So is there a way of making a fraction like this easier to understand or manage? Well Yes. Look again at the numbers and you may notice that both the numerator and denominator are both divisible by 9. This means that they have an equivalent fraction.
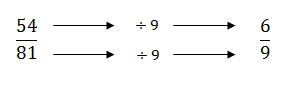
That looks much simpler but is it possible to reduce the number further and making the fraction even simpler. As we have seen above, in the equivalency section, 6/9 does have a smaller equivalent fraction as both the numerator, the 6, and the denominator, 9, are divisible by 3.
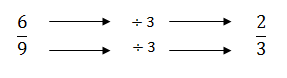
That seems much easier to manage. The fraction of 54/81 is the same fraction as 2/3. But can we reduce it further? No. We can divide the numerator, 2, by 2 and we get one but if we try the same with the denominator, 3, we would end up with 1.5 and numerators and denominators have to be whole numbers.
So we have found the lowest equivalent fraction of 54/81 which makes it easier to manage.
Improper Fractions
Improper fractions are when the numerator is larger than the denominator.
For example
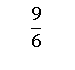
This looks rather difficult at first site but is actually quite simple.
The denominator indicates the how many pieces the whole is divided by and the numerator indicates the amount of those pieces present. So if a pie was cut into six sections, but there were 9 pieces in total, then six of the sections would make one whole pie and another pie would be required for the remaining three pieces.
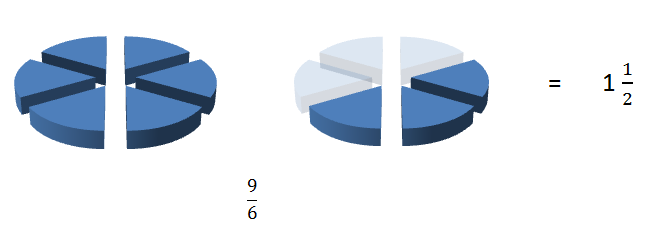
This makes the improper fraction of 9/6 the equivalent of one whole and a half.
Adding Fractions
Adding Fractions with the same denominator
If you had two sets of fractions and wanted to know how much you had in total you would need to add the fractions together. If you had two cakes that had been cut into 8 portions each and one cake had six pieces eaten leaving 2/8’s while another had four pieces eaten leaving 4/8’s, what fraction of whole cakes are remaining.
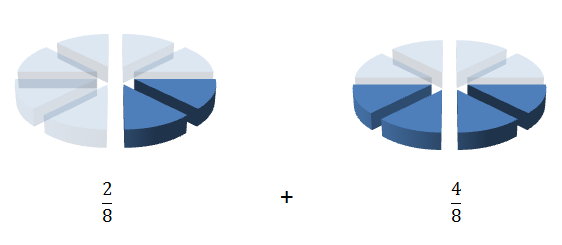
To add the fractions together you simply add the two top numbers together (the top numbers are known as numerators while the bottom numbers are called denominators).
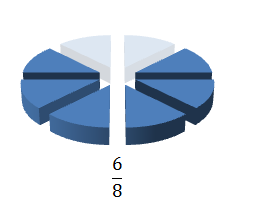
So 2/8 plus 4/8 equals 6/8
Adding Fractions with Different Denominators
Adding fractions together when the denominators are the same is relatively simple but things get a little trickier when they denominators are different.

The first thing you need to do is make both denominators the same and to do this we need to Find The Lowest Denominator. This means finding the lowest common multiple of both denominators. To do this you can list the multiples of each number and find the number that appears in both lists.
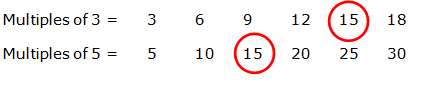
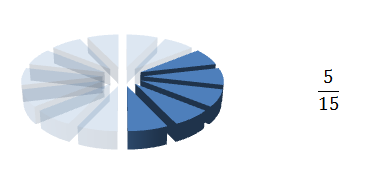
So in this case the lowest common denominator is 15 and this becomes the denominator for both pies. To calculate the numerators you must do the same to each of them as you did to the denominator. So in the case of the first pie you had to multiply the denominator by 5 to get 15 (3 X 5 = 15) and so you must times the numerator also by 5 the first fraction becomes
And the second denominator needed to be multiplied by 3 (5X3 =15) to make 15 so the numerator, 2, also needs to be multiplied by 3 making six so the second fraction becomes.
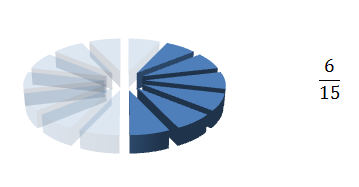
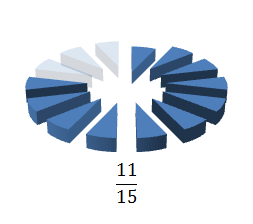
And so the sum becomes

And the answer is
You may notice that the lowest common denominator is the two denominators (3 and 5) multiplied together. This is often the case unless one denominator is a multiple of the other (say 2 and 4) in which case the ‘lowest common denominator’ is the larger of the two numbers (so in the case of 2 and 4 the lowest common denominator is 4).
Subtracting Fractions
Subtracting Fractions with the Same Denominator
If you wish to subtract one fraction from another and both fractions have the same denominator than it is very simple. You simply take one of the numerators away from the other leaving the denominators as they are.
For example
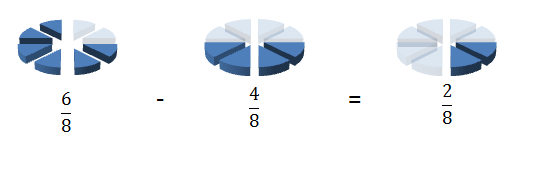
Subtracting Fractions with Different Denominators
If the two fractions have different denominators then you first need to make the denominators the same (with the same method as with adding) by finding the lowest common denominator.
This means finding the lowest common multiple of both denominators. To do this you can list the multiples of each number and find the number that appears in both lists.
So if we are required to calculate the following.
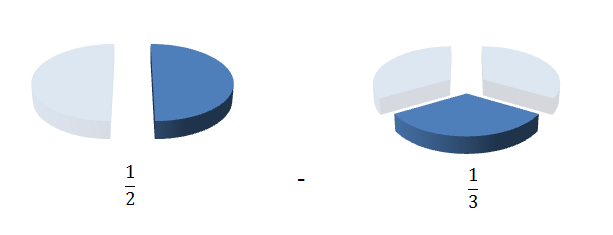
We would then write out the first few multiples of the denominators.
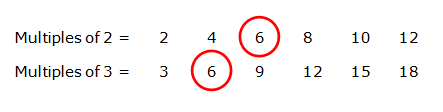
From this we can see that the first number to appear in both sets is the number 6 which is our lowest common denominator. We therefore need to make each fraction have six as its denominator.
As the first fraction of one half would require the denominator (the two) to be multiplied by three in order to make six we must also multiply the numerator (the one) by 3 also.
Now for the second fraction of one third. In order to make this denominator (the three) equal six we must multiply it by two. We must then do the same for the numerator (the 1) to make 2. We have now changed the sum in to the much more manageable version of:-
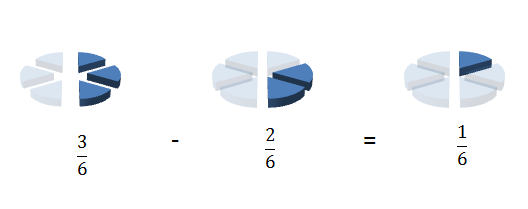
You may notice that the lowest common denominator is the two denominators (2 and 3) multiplied together. This is often the case unless one denominator is a multiple of the other (say 2 and 4) in which case the ‘lowest common denominator’ is the larger of the two numbers (so in the case of 2 and 4 the lowest common denominator is 4).


