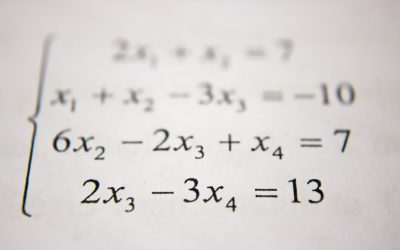➕ Introduction to Mathematics
The Language of Patterns, Logic, and Problem-Solving
Mathematics is the science of numbers, shapes, patterns, and relationships. It provides a universal language to describe the world around us—whether we’re counting, measuring, predicting, or solving complex problems. More than just calculations, maths is a way of thinking: logical, precise, and creative.
At its core, mathematics explores questions like:
-
How do we measure and compare things?
-
What happens when we follow certain rules or operations?
-
How can we predict outcomes or analyse patterns?
-
What structures exist beneath the surface of reality?
Maths is used in every area of life—from calculating a grocery bill to designing bridges, forecasting the weather, or sending spacecraft to Mars. It’s essential in science, engineering, technology, economics, architecture, and even music and art.
Divided into fields such as arithmetic, algebra, geometry, statistics, and calculus, mathematics grows more powerful as we explore deeper concepts. And it’s not just about finding the right answer—it’s about understanding why it’s right, and discovering new ways to think.
Studying maths sharpens our ability to reason, solve problems, and recognise the hidden patterns that shape our world.
Prime Factors
Prime factors are an essential concept in mathematics that play a significant role in various areas of study, including number theory, cryptography, and problem-solving. Understanding prime factors is crucial for solving complex mathematical problems and has practical applications in real life. In this article, we will explore the basics of prime factors, how to find them, their importance in mathematics, their connection to prime numbers, and their applications in different fields. Summary Prime factors are the building blocks of numbers and are essential in mathematics. To find the prime factors of a number, divide it by the smallest prime number until the result is a prime number. Prime factorization is crucial in solving complex problems, such as finding the greatest common divisor or least common multiple. Prime factors play a significant role in cryptography, where they are used to encrypt and decrypt messages. Prime factors have practical applications in real life, such as in computer science and engineering. Understanding the Basics of Prime Factors Prime factors are the prime numbers that divide a given number evenly without leaving a remainder. In other words, they are the building blocks of a number. For example, the prime factors of 12 are 2 and 3 because 2 × 2 × 3 = 12. Prime factors are always prime numbers themselves and cannot be further divided into smaller whole numbers. Properties of prime factors include the fact that every positive integer greater than 1 can be expressed as a product of prime factors in a unique way. This is known as the fundamental theorem of arithmetic. Additionally, the prime factorization of a number...
Prime Numbers
Prime numbers are a fundamental concept in mathematics with a wide range of applications in various fields. They have intrigued mathematicians for centuries due to their unique properties and patterns. In this blog post, we will explore the world of prime numbers, from their definition and properties to their applications in cryptography, computer science, and everyday life. We will also delve into the history of the search for the largest prime number, the role of prime numbers in mathematics and science, and the unsolved problems and current research in prime number theory. Summary Prime numbers are numbers that can only be divided by 1 and themselves. The Sieve of Eratosthenes is a method for finding prime numbers by eliminating multiples of smaller primes. Prime numbers are important in cryptography because they are used to create secure encryption keys. The distribution of prime numbers follows patterns and conjectures, but there is still much research to be done in this area. The largest known prime number has over 24 million digits and was discovered in 2018. What are Prime Numbers and How are They Defined? Prime numbers are natural numbers greater than 1 that have no divisors other than 1 and themselves. In other words, they cannot be divided evenly by any other number except for 1 and the number itself. For example, 2, 3, 5, 7, and 11 are all prime numbers. Prime numbers have several interesting properties. One of the most notable properties is that every natural number greater than 1 can be expressed as a product of prime numbers in a unique way, known as the fundamental...
Multiples
Multiples are an important concept in mathematics that is used to understand and solve various problems. In simple terms, multiples are the numbers that can be divided evenly by another number. For example, the multiples of 3 are 3, 6, 9, 12, and so on. Understanding multiples is crucial in mathematics as it helps in various mathematical operations such as finding factors, simplifying fractions, and determining the least common multiple. Summary Multiples are numbers that can be divided by another number without leaving a remainder. To identify multiples of a number, simply multiply it by other numbers. Prime numbers have only two multiples: 1 and themselves. Common multiples are numbers that are multiples of two or more numbers, while the least common multiple is the smallest common multiple. Multiples have various applications in mathematics, including in fractions, decimals, and ratios. Identifying Multiples of a Number A multiple of a number is any number that can be obtained by multiplying that number by another whole number. For example, the multiples of 4 are 4, 8, 12, 16, and so on. To find the multiples of a number, you can simply multiply the number by different whole numbers and list down the results. Identifying multiples is important in problem solving as it helps in determining patterns and relationships between numbers. For example, if you are trying to find the next number in a sequence, knowing the multiples of a certain number can help you identify the pattern and predict the next number. Multiples of Prime Numbers Prime numbers are numbers that are only divisible by 1 and themselves. Examples of prime...
Estimation and accuracy
Estimation is the process of predicting or approximating a value or outcome based on available information. It is an essential aspect of decision-making in various fields, including business and industry. Accuracy in estimation refers to the degree of closeness between the estimated value and the actual value. Accurate estimation is crucial as it provides a foundation for making informed decisions and planning for the future. Summary Estimation is the process of predicting or approximating a value or outcome. Accurate estimation is crucial for success in business and industry. There are various techniques for estimation, including expert judgement and statistical analysis. Factors that affect estimation accuracy include data quality, assumptions, and biases. Common errors in estimation can be avoided by using multiple techniques and validating assumptions. Importance of Accurate Estimation in Business and Industry Inaccurate estimation can have significant consequences for businesses and industries. It can lead to financial losses, missed deadlines, and poor resource allocation. For example, if a construction project is estimated to take six months but ends up taking a year, it can result in increased costs, delayed revenue generation, and damage to the company’s reputation. Accurate estimation, on the other hand, enables businesses to make realistic plans, allocate resources effectively, and meet customer expectations. Accurate estimation also has several benefits for businesses and industries. It allows for better budgeting and cost control, as organizations can accurately predict expenses and allocate funds accordingly. It helps in resource management by ensuring that the right amount of resources is allocated to each task or project. Accurate estimation also enables businesses to set realistic goals and timelines, which increases the...
Calculations with money
Understanding money calculations is an essential skill that everyone should possess. Whether you are managing your personal finances, running a business, or simply making everyday purchases, being able to accurately calculate and understand money is crucial. In this article, we will explore various aspects of money calculations, including currency denominations, basic arithmetic operations, discounts and sale prices, VAT calculations, currency conversion, interest rates and loan repayments, budgeting and managing personal finances, income tax calculations, profit and loss calculations in business transactions, and the use of spreadsheets and financial software for money calculations. Summary UK currency denominations include pounds (£), pence (p), and notes of various values. Basic arithmetic operations for money calculations include addition, subtraction, multiplication, and division. To calculate discounts and sale prices, subtract the discount percentage from the original price. VAT (Value Added Tax) is a tax on goods and services in the UK, currently set at 20%. Converting currencies for international transactions involves using exchange rates to determine the value of one currency in another. Understanding currency denominations in the UK In the United Kingdom, the currency is the British pound (£). The pound is divided into 100 pence (p). The commonly used coins in the UK are the 1p, 2p, 5p, 10p, 20p, 50p, £1, and £2 coins. The notes in circulation are £5, £10, £20, and £50 notes. It is important to familiarize yourself with these denominations to ensure that you can accurately identify and use them in transactions. To identify different denominations of coins and notes, you can look for specific features such as the size, color, and design. For example, the £1...
Order of Operations
The Order of Operations is a set of rules that dictate the sequence in which mathematical operations should be performed in an equation or expression. It ensures that calculations are done consistently and accurately, regardless of the complexity of the problem. The purpose of the Order of Operations is to eliminate ambiguity and provide a standard method for solving mathematical problems. Summary The Order of Operations is a set of rules for solving mathematical expressions. Following the correct Order of Operations is crucial to getting the right answer. Common mistakes include forgetting to use parentheses and not understanding the hierarchy of operations. Parentheses are used to indicate which operations should be done first. Exponents have the highest priority in the Order of Operations. Understanding the basics of the Order of Operations The acronym PEMDAS is commonly used to remember the order of precedence in the Order of Operations. It stands for Parentheses, Exponents, Multiplication and Division (from left to right), and Addition and Subtraction (from left to right). This means that calculations within parentheses should be done first, followed by any exponents, then multiplication and division, and finally addition and subtraction. For example, in the expression 2 + 3 x 4 – 5, according to PEMDAS, we would first perform the multiplication (3 x 4 = 12), then the addition (2 + 12 = 14), and finally the subtraction (14 – 5 = 9). If we were to perform the operations in a different order, we would get a different result. The importance of following the correct Order of Operations Following the correct Order of Operations is crucial for...
Mental Maths
Mental maths is the ability to perform calculations in your head without the use of any external tools, such as a calculator or pen and paper. It is an important skill to have as it allows individuals to solve problems quickly and efficiently. Mental maths is not only useful in academic settings, but also in everyday life. From budgeting and financial planning to time management and cooking, mental maths plays a crucial role in various aspects of our lives. Summary Mental maths is the ability to perform calculations in your head without the use of a calculator or written methods. It is important because it helps to improve problem-solving skills, boosts confidence, and enhances overall mathematical ability. Regular practice of mental maths can lead to improved memory, faster thinking, and increased accuracy. Mental maths can be applied to everyday situations such as calculating change, budgeting, and measuring ingredients in cooking. Children can benefit from mental maths strategies such as using visual aids and breaking down problems into smaller parts, while adults can use techniques such as estimation and approximation. What is Mental Maths and Why is it Important? Mental maths refers to the ability to perform calculations mentally, without the use of any external aids. It involves using mental strategies and techniques to solve mathematical problems quickly and accurately. Mental maths is important because it allows individuals to solve problems on the spot, without having to rely on external tools. It helps develop critical thinking skills, improves memory and concentration, and boosts confidence. Tips and Tricks for Improving Mental Maths Skills 1. Practice regularly: Like any other skill, mental...
Dividing by 10, 100 and 1000
Understanding division by 10, 100, and 1000 is an essential skill in mathematics. It allows us to divide numbers by powers of 10, which is a fundamental concept in arithmetic. This skill is not only important for solving mathematical problems but also for everyday life situations such as dividing money or measuring quantities. In this article, we will explore the basics of dividing by 10, 100, and 1000, as well as provide tips and tricks, mental math techniques, and real-life problem-solving examples. Summary Dividing by 10, 100 and 1000 involves moving digits to the right by one, two and three places respectively. To divide by 10, simply remove the last digit; to divide by 100, remove the last two digits; to divide by 1000, remove the last three digits. Mental maths can be used to quickly divide by 10, 100 and 1000 by visualising the movement of digits. When dividing decimal numbers, the decimal point must also be moved to the right by the same number of places as the digits. Dividing fractions, mixed numbers and real-life problems using division by 10, 100 and 1000 follow similar principles as whole numbers. Understanding the basics of dividing by 10, 100, and 1000 To understand division by 10, 100, and 1000, we first need to understand the concept of division itself. Division is the process of splitting a number into equal parts or groups. It is the inverse operation of multiplication. When we divide a number by 10, we are essentially splitting it into ten equal parts. Similarly, when we divide a number by 100, we are splitting it into one...
Multiplying by 10, 100 and 1000
Understanding how to multiply by 10, 100, and 1000 is a fundamental skill in mathematics. It allows us to quickly and efficiently perform calculations involving large numbers, decimals, and fractions. Whether you’re working with whole numbers, decimals, or fractions, knowing how to multiply by these powers of 10 is essential for solving problems in everyday life and in more advanced mathematical concepts. In this article, we will explore the concept of multiplying by 10, 100, and 1000, and provide step-by-step instructions and examples for each scenario. Summary Multiplying by 10, 100 and 1000 involves adding zeros to the end of a number. Place value is important when multiplying by 10, 100 and 1000 as each digit moves to a different place. To multiply whole numbers by 10, 100 and 1000, simply add the appropriate number of zeros to the end of the number. When multiplying decimals by 10, 100 and 1000, move the decimal point to the right by the appropriate number of places. To multiply fractions by 10, 100 and 1000, multiply the numerator by the appropriate number and keep the denominator the same. Understanding the Concept of Multiplying by 10, 100, and 1000 Multiplying by 10, 100, and 1000 involves increasing a number’s value by moving the digits to the left in the place value chart. When we multiply a number by 10, we move all the digits one place to the left. When we multiply by 100, we move all the digits two places to the left. And when we multiply by 1000, we move all the digits three places to the left. For example, if...
Written Division
Written division is a mathematical operation that involves dividing one number by another to find the quotient. It is an essential skill in mathematics and is used in various real-life situations, such as dividing a group of objects equally or calculating the cost per unit. Learning written division is important as it helps develop problem-solving skills, logical thinking, and numeracy. To understand written division, it is essential to be familiar with some basic terms and concepts. The dividend is the number being divided, while the divisor is the number by which the dividend is divided. The quotient is the result of the division, and the remainder is any amount left over after dividing as much as possible. For example, in the division problem 15 ÷ 3 = 5, 15 is the dividend, 3 is the divisor, 5 is the quotient, and there is no remainder. Summary Written division is a method of dividing numbers using a written algorithm. The four steps of written division are divide, multiply, subtract, and bring down. Tips for mastering written division include practicing regularly and breaking down problems into smaller parts. Common mistakes to avoid in written division include forgetting to carry over numbers and not double-checking your work. Written division can be used to solve real-world problems, such as dividing a group of items evenly among people. The Four Steps of Written Division: A Comprehensive Guide Performing written division involves following a set of steps to find the quotient and remainder. Here is a step-by-step guide on how to perform written division: Step 1: Divide– Start by dividing the first digit of the...
Division
Division is a fundamental operation in mathematics that involves splitting a quantity into equal parts. It is the inverse operation of multiplication and is used to find out how many times one number can be divided by another. Division is an essential skill that is used in everyday life, from dividing a pizza among friends to calculating the cost per unit of a product. Without division, it would be difficult to solve many real-life problems and make sense of numerical relationships. Summary Division is a mathematical concept that involves splitting a number into equal parts. It is a basic arithmetic operation that is used in everyday life, from sharing food to calculating budgets. Division plays a crucial role in problem-solving, helping us to find solutions to complex mathematical equations. There are different methods of division, including long division and short division, which can be used depending on the situation. Division is closely related to multiplication, with the two operations working together to solve mathematical problems. Division as a basic arithmetic operation Division is a basic arithmetic operation that allows us to distribute or allocate quantities equally. It involves dividing a dividend by a divisor to obtain a quotient. The dividend is the total quantity being divided, the divisor is the number by which the dividend is divided, and the quotient is the result of the division. For example, if we have 12 apples and want to divide them equally among 3 people, we would divide 12 by 3 to get a quotient of 4. This means each person would receive 4 apples. There are some basic division facts that...
Written Multiplication
Written multiplication is a fundamental mathematical operation that involves multiplying two or more numbers together using a written method. It is an essential skill that is used in everyday life, from calculating prices and discounts to measuring ingredients for recipes. Understanding the basics of written multiplication is crucial for building a strong foundation in mathematics. Written multiplication is the process of multiplying numbers using a written method, such as the traditional vertical method or the lattice method. It involves understanding place value and the relationship between digits in order to accurately multiply numbers together. This skill is used in various mathematical operations, such as finding the area of a rectangle or solving algebraic equations. In everyday life, written multiplication is used in a wide range of situations. For example, when shopping, we often need to calculate the total cost of multiple items or determine the discounted price of an item. In cooking, we use multiplication to adjust recipes based on the number of servings we need. Understanding written multiplication allows us to solve these real-life problems efficiently and accurately. Summary Written multiplication is a fundamental concept in mathematics that involves multiplying numbers using a written method. Learning written multiplication is important for developing strong mathematical skills and problem-solving abilities. To master written multiplication, it is essential to follow a step-by-step guide and practice regularly. Tips and tricks such as breaking down numbers and using mental math can help make written multiplication more efficient. Common mistakes to avoid in written multiplication include forgetting to carry over digits and misplacing decimal points. The Importance of Learning Written Multiplication in Mathematics Written...