Multiplication is a fundamental mathematical operation that involves combining two or more numbers to find their total value. It is often represented by the symbol “x” or “*”, and the result of a multiplication operation is called the product. For example, multiplying 3 by 4 gives a product of 12.
Basic multiplication facts are essential to understanding and solving more complex mathematical problems. These facts include the multiplication tables from 1 to 10, which are often memorized by students to improve their speed and accuracy in calculations. For example, knowing that 7 multiplied by 8 equals 56 can be useful in various situations, such as calculating the total cost of buying 8 items at a price of £7 each.
Symbols and terminology used in multiplication include the multiplication sign “*”, which indicates that two or more numbers are being multiplied together. The numbers being multiplied are called factors, and the result is called the product. For example, in the equation 5 * 6 = 30, 5 and 6 are the factors, and 30 is the product.
Summary
- Multiplication is the process of repeated addition and is a fundamental concept in mathematics.
- Memorizing multiplication tables can be made easier by using tricks such as skip counting and visual aids.
- Multiplication is used in everyday life, from calculating grocery bills to determining the area of a room.
- Division is the inverse operation of multiplication and can be used to solve problems involving equal sharing or grouping.
- Multiplication can be used to simplify complex calculations involving fractions, such as finding a common denominator.
Mastering Multiplication Tables: Tips and Tricks
Memorizing multiplication tables can be challenging for some students, but there are several techniques that can make the process easier. One popular method is using mnemonic devices, such as songs or rhymes, to help remember the multiplication facts. For example, a common rhyme for remembering the multiples of 9 is “9 times 1 is 9, 9 times 2 is 18,” and so on.
Tricks can also be used to solve difficult multiplication facts quickly. For example, multiplying any number by 10 can be done by simply adding a zero to the end of the number. Similarly, multiplying any number by 5 can be done by dividing it in half and then adding a zero. These tricks can save time and improve efficiency in calculations.
Practice exercises are crucial for mastering multiplication tables. Students should regularly practice solving multiplication problems to reinforce their understanding and improve their speed and accuracy. This can be done through worksheets, online exercises, or flashcards. Regular practice will help students become more confident in their multiplication skills.
The Importance of Multiplication in Everyday Life
Multiplication is used in various daily activities, such as calculating the total cost of groceries, determining the amount of ingredients needed for a recipe, or figuring out the distance traveled based on speed and time. For example, if a bag of apples costs £2 and you want to buy 5 bags, you can use multiplication to find that the total cost will be £10.
Multiplication is also important in many career fields. For example, architects use multiplication to calculate the dimensions of buildings, engineers use it to design structures, and scientists use it to analyze data and conduct experiments. Without a solid understanding of multiplication, it would be challenging to excel in these professions.
Real-world applications of multiplication can be seen in various scenarios. For instance, when planning a road trip, multiplication can be used to calculate the total distance traveled based on the average speed and time spent driving. In finance, multiplication is used to calculate interest rates, compound interest, and investment returns. Understanding multiplication is essential for making informed decisions in these situations.
Multiplication and Division: The Relationship Explained
Division is the inverse operation of multiplication. It involves splitting a number into equal parts or groups. For example, dividing 12 by 3 means finding out how many groups of 3 can be made from 12. The result of a division operation is called the quotient.
The relationship between multiplication and division can be understood through the concept of fact families. Fact families are a set of related multiplication and division facts that involve the same numbers. For example, the fact family for the numbers 4, 2, and 8 includes the multiplication facts 4 x 2 = 8 and 2 x 4 = 8, as well as the division facts 8 ÷ 2 = 4 and 8 ÷ 4 = 2.
Examples and practice problems can help reinforce the relationship between multiplication and division. For example, if you know that 7 x 3 = 21, you can use this fact to solve the division problem 21 ÷ 7 = ?. By understanding the relationship between these operations, students can become more proficient in solving mathematical problems involving multiplication and division.
Multiplication and Fractions: Simplifying Complex Calculations
Multiplying fractions involves multiplying the numerators (top numbers) together and multiplying the denominators (bottom numbers) together. The resulting fraction may need to be simplified by reducing it to its lowest terms. For example, multiplying 2/3 by 3/4 gives a product of (2 x 3) / (3 x 4) = 6/12, which can be simplified to 1/2.
Multiplying mixed numbers involves converting them into improper fractions, multiplying them as fractions, and then converting the result back into a mixed number if necessary. For example, multiplying 1 and 1/2 by 2 and 1/4 can be done by converting both mixed numbers into improper fractions (3/2 and 9/4), multiplying them (3/2 x 9/4 = 27/8), and then converting the result back into a mixed number (3 and 3/8).
Simplifying fractions is an important skill that can make calculations involving fractions easier. To simplify a fraction, you need to find the greatest common divisor (GCD) of the numerator and denominator and divide both by this number. For example, to simplify the fraction 12/18, you can find that the GCD of 12 and 18 is 6, so dividing both by 6 gives a simplified fraction of 2/3.
Multiplication in Real-World Scenarios: Examples and Applications
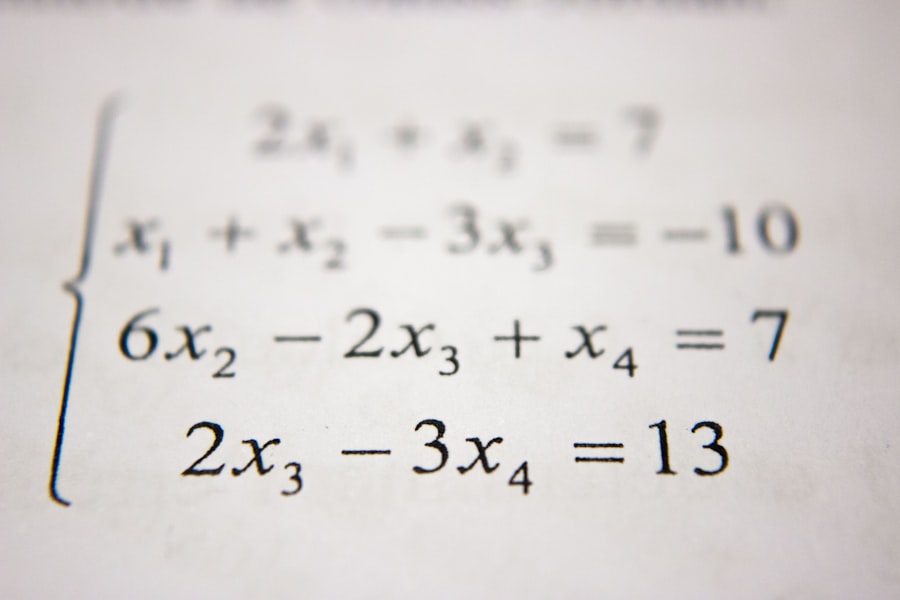
Multiplication has numerous applications in real-world scenarios, including business and finance, science and engineering, and sports and gaming.
In business and finance, multiplication is used to calculate profits, expenses, and revenue. For example, a business owner may use multiplication to determine the total cost of producing a product by multiplying the cost per unit by the number of units produced. Similarly, investors use multiplication to calculate returns on investments or to determine the future value of their savings.
In science and engineering, multiplication is used to analyze data, conduct experiments, and solve complex equations. For example, scientists may use multiplication to calculate the concentration of a substance in a solution or to determine the rate of change in a physical process. Engineers use multiplication to design structures, calculate forces, and analyze systems.
In sports and gaming, multiplication is used to calculate scores, statistics, and probabilities. For example, in basketball, players’ shooting percentages are calculated by dividing the number of successful shots by the total number of shots attempted. Similarly, in card games or gambling, probabilities can be calculated using multiplication to determine the likelihood of certain outcomes.
Mental Math Strategies for Multiplication: Speed and Accuracy
Mental math techniques can help improve speed and accuracy in multiplication calculations. One technique is breaking down larger numbers into smaller factors that are easier to multiply mentally. For example, instead of multiplying 8 by 7 directly, you can break it down into (8 x 5) + (8 x 2) = 40 + 16 = 56.
Another technique is using known multiplication facts to solve more complex problems. For example, if you know that 6 x 7 = 42, you can use this fact to solve the problem 6 x 70 by multiplying 42 by 10. This can save time and make calculations more efficient.
Regular practice is essential for improving mental math skills in multiplication. Students should engage in activities that require mental multiplication, such as solving multiplication problems without using paper or a calculator. This can be done through timed exercises, mental math games, or daily mental math challenges.
Multiplication in Primary Education: Teaching Methods and Resources
Introduction to multiplication in primary education typically begins with teaching the concept of repeated addition. For example, students may be introduced to multiplication by understanding that 3 x 4 means adding 3 four times: 3 + 3 + 3 + 3 = 12.
Teaching methods for multiplication in primary education often involve hands-on activities and visual aids. For example, students may use manipulatives, such as counters or blocks, to represent the numbers being multiplied. This helps them develop a concrete understanding of the concept before moving on to abstract representations.
Resources for teaching multiplication in primary education include textbooks, workbooks, and online resources. Many educational websites offer interactive games and activities that make learning multiplication fun and engaging for young learners. Teachers can also create their own lesson plans and worksheets tailored to the needs of their students.
Multiplication and Technology: Tools for Enhanced Learning
Technology has revolutionized the way multiplication is taught and learned. Online resources and apps provide interactive lessons, practice exercises, and instant feedback to help students improve their multiplication skills. These resources often include visual representations, animations, and step-by-step explanations to make learning more engaging and accessible.
Interactive games and activities are another way technology enhances learning multiplication. These games often incorporate elements of gamification, such as rewards or levels, to motivate students and make learning more enjoyable. They can be played on computers, tablets, or smartphones, allowing students to practice multiplication anytime and anywhere.
Technology is also being integrated into the classroom to enhance multiplication instruction. Interactive whiteboards, tablets, and educational software allow teachers to create dynamic lessons and provide individualized instruction. These tools can help students visualize multiplication concepts, practice skills, and receive immediate feedback, leading to improved learning outcomes.
Advancements in Multiplication: New Techniques and Discoveries
Advancements in multiplication include new techniques and discoveries that make calculations faster and more efficient. For example, the lattice multiplication method is a visual technique that simplifies the process of multiplying large numbers. It involves creating a grid and filling in the products of the digits being multiplied.
New discoveries in multiplication also include algorithms for multiplying large numbers using fewer steps. For example, the Karatsuba algorithm is a fast multiplication algorithm that reduces the number of multiplications required to multiply two numbers. This algorithm is used in computer science and cryptography to perform efficient calculations.
Advancements in teaching methods for multiplication include research-based strategies that improve learning outcomes. For example, the use of manipulatives, visual representations, and real-world applications has been shown to enhance students’ understanding of multiplication. Additionally, incorporating technology into instruction has opened up new possibilities for personalized learning and adaptive instruction.
The future of multiplication holds exciting possibilities, such as the development of new algorithms and techniques that further streamline calculations. As technology continues to advance, we can expect to see more innovative tools and resources that make learning multiplication more accessible and engaging for students of all ages.
Multiplication is a fundamental mathematical operation that plays a crucial role in everyday life. Understanding the basics of multiplication, mastering multiplication tables, and recognizing its importance in various fields are essential for success in mathematics and beyond. By exploring real-world applications, understanding the relationship between multiplication and division, and utilizing mental math strategies, students can become proficient in multiplication and develop valuable problem-solving skills. With advancements in teaching methods and technology, the future of multiplication holds exciting possibilities for enhanced learning and improved efficiency in calculations.
FAQs
What is multiplication?
Multiplication is a mathematical operation that involves combining two or more numbers to get a product. It is represented by the symbol “x” or “•”.
What are the basic rules of multiplication?
The basic rules of multiplication include the commutative property, associative property, and distributive property. The commutative property states that the order of the numbers being multiplied does not affect the product. The associative property states that the grouping of the numbers being multiplied does not affect the product. The distributive property states that multiplying a number by a sum is the same as multiplying the number by each addend and then adding the products.
What are some common multiplication tables?
The most common multiplication tables are the times tables from 1 to 12. These tables are used to memorize the products of the numbers from 1 to 12.
What are some real-life applications of multiplication?
Multiplication is used in many real-life situations, such as calculating the total cost of items when shopping, determining the area of a rectangular room, and calculating the distance traveled by a vehicle given its speed and time.
What are some common mistakes made in multiplication?
Common mistakes made in multiplication include forgetting to carry over when multiplying multi-digit numbers, misplacing decimal points when multiplying decimals, and forgetting to multiply by zero when necessary.

