Binding Energy is the energy required to break up the bonds of atoms or the energy released when small atoms combine.
Binding Energy
This is the energy required to break up the bonds of atoms or the energy released when small atoms combine.
There are two types of binding energy including electron binding energy (the energy required to overcome the electromagnetic force holding the electrons in orbit) and the Nuclear Binding Energy.
Nuclear Binding Energy
This can be thought of as either; the energy required to break up the bonds of the nucleus of an atom or the energy released when nucleons combine.
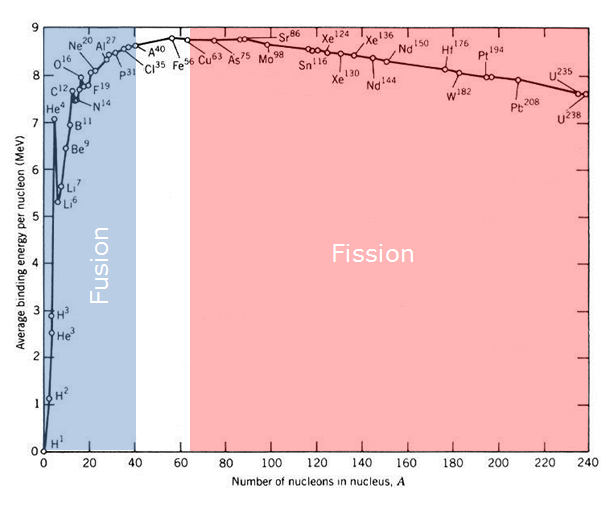
The table above shows the amount of binding energy in each nucleon of each element. The higher binding energy per nucleon the more stable the nucleus of the element is and all elements want to be as stable as possible. As you can see from the table Iron is the most stable (has the most b-energy per nucleon) element and as such neither nuclear fusion nor fission is possible. As you can see from the table, all elements with less mass then iron will release energy through nuclear fusion as these element gain nuclear b-energy per nucleon as their mass increases. Elements with more mass than iron have less b-energy per nucleon and so they release energy from splitting into less massive elements through nuclear fission.
Calculating Binding Energy
A nucleus – except in the case of hydrogen which contains a single proton – has less mass than that of its individual parts combined. So a helium nucleus, containing two neutrons and two protons, has less mass then the individual protons and neutrons added together.
The difference between the total mass of the nucleus and its individual nucleons (protons and neutrons) is equal to the nuclear binding energy.
Particle
Mass (u)
Proton
1.0073
Neutron
1.0086
The mass is shown in atomic mass units (u) which are equal to 1.661 x 10-27 kg or 931.3 MeV
To calculate the binding energy we first need to determine the mass deficit which requires the assumed mass of the nucleus and the actual mass of the nucleus.
Calculating the Assumed Mass
This can be done by working out the amount of protons and neutrons in the nucleus. Then multiply those by their mass using the table above and this will give you the assumed mass of the nucleus.
For Example
He4 has 2 protons (2 x 1.0073 = 2.0146) and 2 neutrons (2 x 1.0086 = 2.0172) so the assumed mass of the nucleus would be 4.0318 (u).
The actual mass of He4 nucleus is 4.001505 u which gives us a deficit mass of 0.030377 u
1 atomic mass unit (u) is equal to 931.3 MeV so
Binding Energy = 931.5 MeV x Mass Deficit
So in the case of He4 the binding energy can be calculated by multiplying 931.3 by 0.030377 so the binding energy of a He4 nucleus would be 28.30 MeV.
Binding Energy per Nucleon
To calculate the binding Energy per nucleon we simply divide the b-energy of the nucleus by the amount of nucleon so in the case of He4 the b-energy per nucleon is 28.30 MeV / 4 nucleons = 7.075 MeV.